Qs = 0.0112(Q)2.67(Qbf)-1.67
Qs = Bedload transport (kg/sec)
Q = Flow (cms)
Qbf = Bankfull flow (cms)
Units of constant = kg/m3
This equation may be used to estimate average bedload transport over time and space for gravel bed streams and rivers in dynamic equilibrium and having a bed gradient equal to the hydraulic gradient (see paper for full equation addressing differences in bed and hydraulic slope). Derivation of the equation is described at https://ascelibrary.org/doi/10.1061/JHEND8.HYENG-12983 (open source).
Background:
I have long been fascinated by the physical geometry and formative processes of river channels striving to understand what dictates the dimensions of a channel and what makes the channel take a circuitous route down a valley. Over many years of practice in field of river mechanics I have learned a lot but have been frustrated with one aspect, bedload transport. Many theories have been presented to quantify bedload transport over the past 100-years. Theories have been developed using physical properties, empirical methods, and stochastic methods (random statistical probability). In general the theories based on physical properties include an empirically derived “pickup probability” term to account for the fact than not all river bed particles capable of being transported by river flow are transported. Most empirical theories have been developed subject to some physical basis. Stochastic methods are statistical approximations. A recent evaluation of theories based on physical properties and empirical methods demonstrated that the empirically derived theories are far better at quantifying bedload transport than the theories based on physical properties but plots of computed vs. measured bedload transport even for the empirically derived methods are not balanced around a line of perfect agreement throughout the range of data. (Hinton, et.al., 2018, Comparison of Calibrated Empirical and Semi-Empirical Methods for Bedload Transport Rate Prediction in Gravel Bed Streams - https://ascelibrary.org/doi/abs/10.1061/%28ASCE%29HY.1943-7900.0001474). The recommended practice for use of bedload transport theories for prediction of bedload has consisted of selecting an equation or equations developed using data from a stream or river similar to the channel of interest then evaluating the results for confidence. This approach left me with little confidence in the available theories hence my interest in exploring the possibility of finding a new relationship that would estimate bedload transport with greater confidence or at least allow me to learn more about the shortcomings of available theories.
Development of Regime Channel Bedload Transport Equation:
Accommodating the new investigation was a recently published large database of bedload measurements including hydraulic, channel, and bed sediment data (Hinton, et.al., Comprehensive and Quality Controlled Bedload Transport Database - https://ascelibrary.org/doi
/abs/10.1061/%28ASCE%29HY.1943-7900.0001221). Although this database includes some unstable channels as well as many regime channels, an adequate number of data sets containing bedload transport data, bed material data, and bankfull channel data are available to characterize regime channel bedload transport. With a single exception of which I am aware all bedload transport theories have been developed using individual bedload measurements at one to a few sites and/or using flume studies. Only one bankfull data point can be derived from bedload measurements at each site and no bankfull data point can be derived from flume data. Consequently the methods used to develop presently available theories of bedload transport have precluded the use of bankfull hydraulic characteristics as a factor.
Being aware of common references to bankfull hydraulic conditions as a significant factor of bedload transport, I choose to evaluate bedload transport using a form of data capable of characterizing bankfull hydraulic conditions. This required employing data from many sites, each site representing one bankfull data point. The coefficients and exponents of sediment rating curves developed from individual measurements include a point representing bankfull hydraulic conditions and were therefore employed as data for regression against reported bankfull hydraulic data. The derivation included exponential rotations, an application of game theory in its ubiquitous form, for a constant exponent of stream power and a minor exponential rotation was employed on the exponent of bankfull stream power for the regime channel bedload transport equation to be dimensionally homogeneous.
Sensitivity Analysis:
The exponent in the numerator of the regime channel bedload transport equation, 2.67, was determined as the average of the exponents in the analysis data set sediment rating curves (“stream equations” in paper). The average of exponents in the smaller verification data set is 2.47. Troendle’s Relative Relationship relies on an exponent of 3.08. A sensitivity analysis of the numerator and denominator (numerator exponent minus one) was conducted to better understand the significance and value of the exponents. The statistical performance of the regime channel bedload transport equation was found to start dropping off above exponents of 2.85/1.85 and below exponents of 2.50/1.50. Hence if a physically based model is found to reproduce the regime channel bedload transport equation, the exponents will fall within the range of 2.50/1.50 and 2.85/1.85 and not necessarily be 2.67/1.67.
Application for Further Research:
Although bankfull hydraulic characteristics have been alluded to in prior literature as a factor in bedload transport, the regime channel bedload transport equation proves that bankfull hydraulic characteristics are a primary factor in bedload transport serving to buffer potential bedload transport estimates based solely on stream power. The regime channel bedload transport equation reflects the channel forming influence of the hydrologic regime characterized by stream power in the numerator buffered by geologic resistance characterized by bankfull stream power in the denominator. Physical properties governing transport of individual bed particles include particle characteristics (size, exposure and density), boundary shear stress, and momentum of water. Use of the regime channel bedload transport equation for a complete understanding of the physical processes governing bedload transport becomes a question of what factor or factors of bankfull stream power (or bankfull flow for the case of bed slope equals hydraulic gradient) are capable of characterizing bankfull hydraulic characteristics and are also factors of physically based bedload transport processes. The relative roughness of the bed being substantially dictated by bankfull hydraulic characteristics and being responsible for channel geometry and ultimately hydraulic slope thus boundary shear stress and momentum of water stands out as the primary factor connecting bankfull hydraulic conditions and the physical processes governing bedload transport. Relative roughness of the bed is also a function of the soil matrix through which the channel passes.
Use of the regime channel bedload transport equation as a basis for derivation of a physically based relationship quantifying bedload transport may be possible by replacing bankfull flow in the equation by a resistance based equation for flow such as the Manning’s or Chezy equation and replacing the roughness coefficient or factor with relative roughness. This will introduce an effective bed particle size into the regime channel bedload transport relationship allowing further research toward finding a complete physically based bedload transport relationship. Due to ambiguities associated with roughness this will not be a simple task.
Application for Annual and Average Annual Bedload:
The regime channel bedload transport equation may be used to estimate annual and average annual bedload by integrating the regime channel bedload transport equation over an annual or average annual flow-duration curve. The result, however, will overlook times of no bedload transport and will assume bedload transport occurs in the overbank floodplains. Both conditions will result in less bedload transport than calculated using a full flow-duration curve. If the flow representing the threshold of bedload transport is known, the integration can be limited to flow above the threshold of transport. Likewise, if the portion of high flow conveyed in the overbank floodplains is known, it may be subtracted from total flow for the purpose of calculating bedload transport at times of high flow. If these data are not known, it is helpful to know the significance of potential bedload transport error.
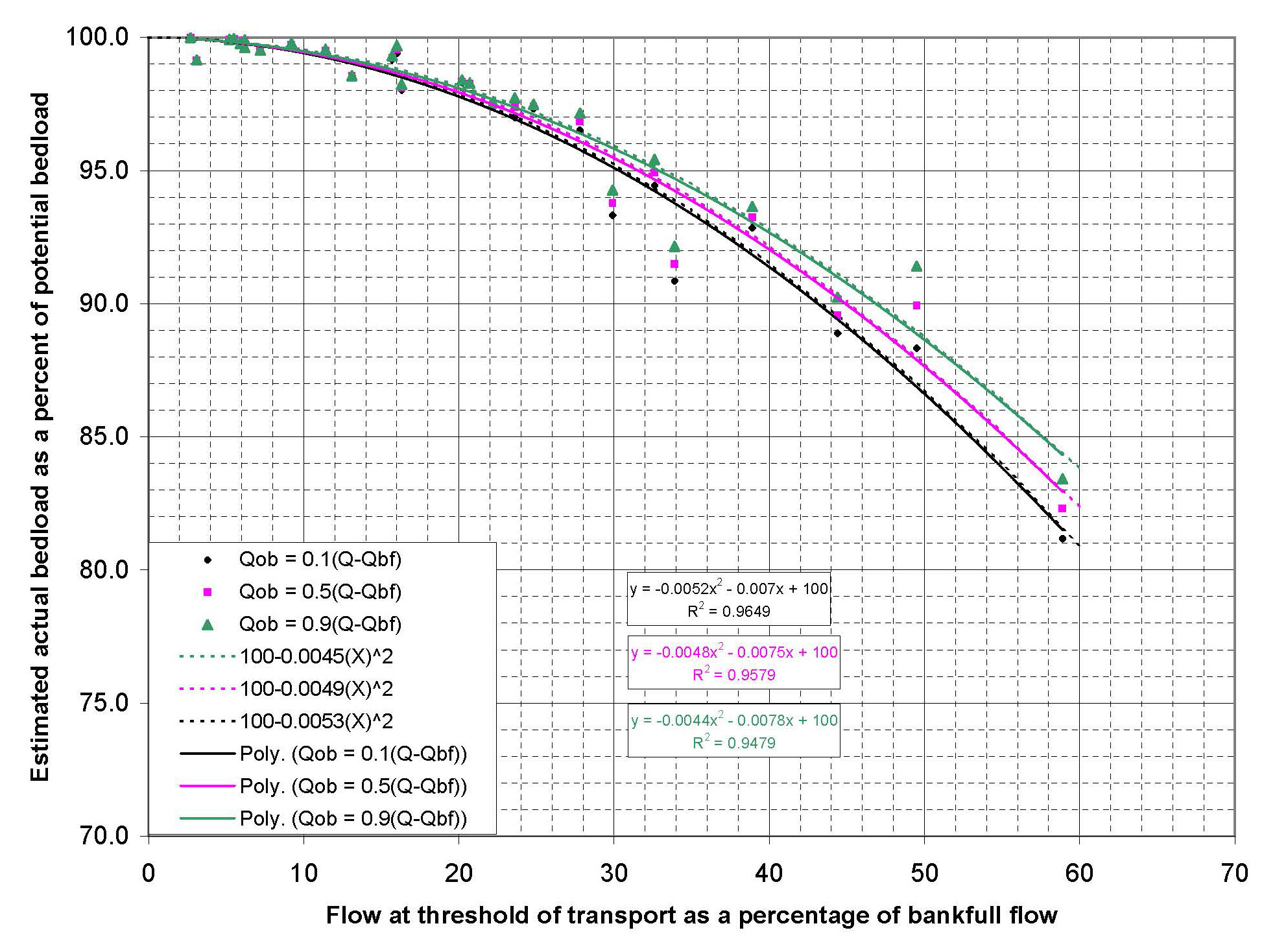
In order to develop an understanding of potential bedload transport error associated with inability to account for threshold of bedload transport and overbank flow, I conducted an analysis using all analysis and verification sites employed for development of the regime channel bedload transport equation for which flow-duration curve data are available on the USGS Streamstats web application, a total of 27-sites. The analysis consisted of calculating an estimate of actual average annual bedload transport assuming a threshold of transport at each site and assuming three conditions of overbank flow. The flow for which the lowest bedload transport measurement was recorded was assumed to be the threshold of bedload transport. This is a very defensible assumption. Although it is safe to assume that the highest bedload transport measurements in the database were most likely conducted at times when significant overbank flow was not present, knowledge of the actual overbank flows at the sites is not well represented in the database. Consequently, for the purpose of analysis, overbank flows were assumed to be 0.1, 0.5, and 0.9 times the flow in excess of reported bank full flow. This represents conditions of 10-, 50-, and 90- percent of flow in excess of reported bank full flow being conveyed in the overbank floodplains respectively, the former having a minimal overbank floodplain and the later having extensive wide, flat overbank floodplain. The estimated actual bedload transport as a portion of total potential bedload transport (without considering threshold of transport or overbank flow) was plotted against flow at the threshold of bedload transport as a percentage of bankfull flow. The result produced the remarkably consistent result identified in Figure 1.
Several conclusions can be derived from this analysis. First, the threshold of bedload transport for sites investigated is much lower than bankfull flow. Second, the significance of overbank flow to estimation of annual or average annual bedload transport is very minor. Finally, even if the flow representing the threshold of bedload transport is on the order of half of bankfull flow (high threshold), the estimate of annual or average annual bedload transport will be within 15-percent of potential annual or average annual bedload transport, a small error when considering the precision of bedload transport estimates in general.